ARM 算子性能优化上手指南-博客-MegEngine

前言

做 arm 侧算子开发时，不能不关心的就是性能。本文主要就是介绍 arm 算子性能优化的常用思路，做为一个入门级的参考。文章以 ARM Cortex a55 上的 GaussianBlur 优化为例展开，并在文末对 arm 性能优化思路做了一个总结。

GaussianBlur 的优化

Q1: 什么是 GaussianBlur?

GaussianBlur 是一种线性平滑滤波。它的计算过程是：原图每一个点都和周边点进行加权求和，得到对应位置的输出，权重矩阵是 kernel。以 kernel_size=3 为例，如图：

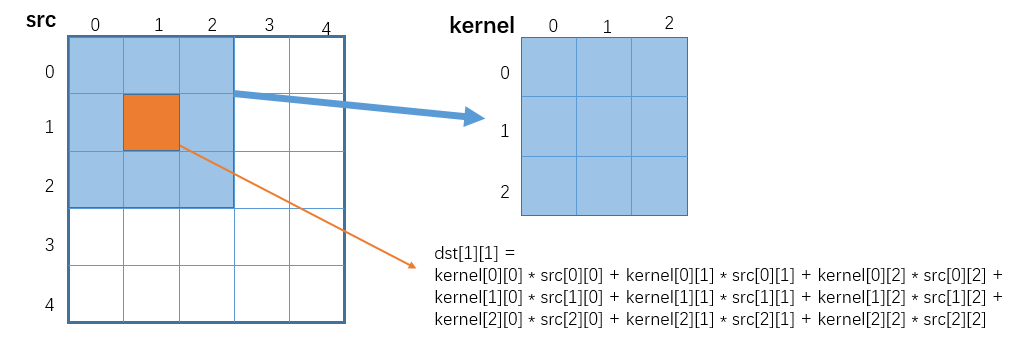
示例代码如下：

// 示例代码 1 
/*
    src : float[h][w]
    kernel : float[3][3]
    受限于篇幅，本文的代码仅做演示，不考虑图像的边界处理
*/
for(int i = 1 ; i < h-1 ; ++i ){
    for(int j = 1 ; j < w-1; ++j){
        dst[i][j] = 
            src[i-1][j-1] * kernel[0][0] + src[i-1][j] * kernel[0][1] + src[i-1][j+1] * kernel[0][2] + 
            src[i][j-1]   * kernel[1][0] + src[i][j]   * kernel[1][1] + src[i][j+1]   * kernel[1][2] +
            src[i+1][j-1] * kernel[2][0] + src[i+1][j] * kernel[2][1] + src[i+1][j+1] * kernel[2][2]
    }
}

而 kernel 的值是由高斯公式 ¹ 算出，并做了归一化。比如常用的 kernel_size=3 的 kernel 为：

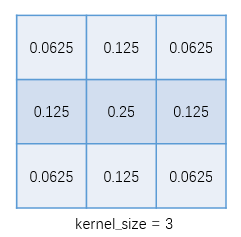
它可以由两个向量相乘得到： $\{0.25, 0.5, 0.25\}^T * \{0.25, 0.5, 0.25\}$ 。

Q2: 如何进行优化？

接下来，笔者将以 kernel_size=3 的 GaussianBlur 为例，介绍一些常见的优化思路：

Point 1：首先考虑算法层面的优化–可分离滤波

根据笔者的经验，性能优化的主要效益来自于算法层面的优化，这是从根本上减少计算量，所以第一步是考虑算法层面的优化。对于高斯滤波来说，它是一个可分离滤波，这意味着

它的 kernel 可以拆成行方向和列方向两个向量的乘积。即 $\{0.25, 0.5, 0.25\}^T * \{0.25, 0.5, 0.25\}$
示例代码 1 的逻辑等效于，先做一个方向的卷积，再做另一个方向的卷积。代码如下：

// 示例代码 2
/* 
    buf : float[3][w], 用来保存行内卷积的中间计算结果
    src ：float[h][w], 输入图像，类型为 F32C1, 高为 h, 宽为 w
    kx : float[3] , x 方向上的卷积
    ky : float[3] , y 方向上的卷积，此处和 kx 相同
*/
// ------------------ 先计算前 2 行的行内卷积，保存到 buf 中  ----------------------
for(int i = 0; i < ksize-1; ++i){
    for(int j = 1; j < w-1 ; ++j ){
        buf[i][j] = src[i][j-1] * kx[0] + src[i][j] * kx[1] + src[i][j+1] * kx[2];
    }
}
// 每算一行新的，凑齐 3 行，做一次行间的卷积。 期间更新 buf
#define IDX(n) (n%3)
for(int i = 1; i < h-1; ++i ){
    for(int j = 1; j < w-1; ++j){
        buf[IDX(i+1)][j] = src[i+1][j-1] * kx[0] + src[i+1][j] * kx[1] + src[i+1][j+1] * kx[2];
        dst[i][j] = buf[IDX(i-1)][j-1] * ky[0] + buf[IDX(i)][j-1] * ky[1] + buf[IDX(i+1)][j-1] * ky[2]; 
    }
}

分析一下：示例代码 1 的时间复杂度为 $O(h * w * kx * ky)$ , 示例代码 2 的时间复杂度为 $O(h * w * (kx + ky) )$ ，可以看到时间复杂度变小了。

简单总结一下：算子优化首先从数学角度出发，看能不能找到等效或者近似的算法来降低算法的复杂度。而类似的 GaussianBlur 的优化思路还有’Stack Blur’ ² （用多个 boxfilter 去模拟 gaussianblur); 转换到频域上计算等。

Point 2：考虑减少重复计算

做完 Point1 算法设计的优化，大幅减少了计算量，但算法实现过程可能会有不少重复计算，所以第二步接着考虑减少重复计算。这里还是以示例代码 2 为例，关注以下几个点：

通过引入 buf 并借助 IDX(n) 宏，复用了前 2 行的行内计算结果。由原先的每做一次行间计算，需要先做 3 次行内计算，变成了每做一次行间计算，只需要做 1 次行内计算。从而减少了计算量
因为buf[i][j] = src[i][j-1] * kx[0] + src[i][j] * kx[1] + src[i][j+1] * kx[2];里 kx[0] 和 kx[2] 都是 0.25。所以可以优化成buf[i][j] = (src[i][j-1] + src[i][j+1] )* kx[0] + src[i][j] * kx[1] ;从而由 3 次乘法 2 次加法变成了 2 次乘法 2 次加法。

简单总结一下：性能优化过程中，需要关注哪些计算是之前做过的，进而设计一个数据结构去缓存复用它。同时关注算法本身的一些特性（比如高斯核是对称的），看看能不能减少一些计算量。

Point 3： SIMD 提高数据级并行度

前 2 步基本保证运算是必需且最少的，第三步就需要考虑提高数据级并行度。

数据级并行（Data Level Parallelism，简称 DLP），主要手段是 SIMD/SIMT，简单理解成一条指令同时处理多个数据。ARM 上主要是使用 NEON 指令集/SVE 指令集。受限于篇幅，以下的示例代码，只拿示例代码 2 中 先计算前 2 行的行内卷积 的部分做演示。

// 示例代码 3
constexpr size_t step = 128/sizeof(float); // 一条 NEON 指令能处理的数据长度为 128bit, 可以并行处理 step 个 float
flaot32x4_t vload[3]; // 暂存 load 的结果，用于向量化计算
float32x4_t k[3];

k[0] = vdupq_n_f32(kx[0]); // k[0] = {0.25, 0.25, 0.25}
k[1] = vdupq_n_f32(kx[1]); // k[1] = {0.5, 0.5, 0.5}
for(int i = 0; i < ksize-1; ++i){
    int j = 1;
    for(; j < w - 1 - step; j += step){
        vload[0] = vld1q_f32(src[i][j-1]);
        vload[1] = vld1q_f32(src[i][j]);
        vload[2] = vld1q_f32(src[i][j+1]);
        float32x4_t tmp = vmulq_f32(vload[1], k[1]);
        float32x4_t vbuf = vmlaq_f32(tmp, k[0], vaddq_f32(vload[0], vload[2]));
        vst1q_f32(buf[i][j], vbuf);
    }
    // 标量处理剩下的部分数据
    for(; j < w-1 ; ++j ){
        buf[i][j] = (src[i][j-1] + src[i][j+1]) * kx[0] + src[i][j] * kx[1];
    }
}

稍微总结一下： 拿到一串代码，可以考虑是否可以进行向量化。

NEON 指令向量化也是有局限的。比如对于一些查表操作，分支操作不好进行向量化。对于 NEON 的查表，可以考虑先标量查表，用查表结果初始化一个向量，以便后继操作的向量化。

另外，在精度误差允许的前提下，可以把 float 量化成 uin8_t, uint16_t 等，或者使用 float16，从而获得更高的并行度。（NEON 指令一次处理 128bit, 可以一次性处理 16 个 uint8_t，8 个 uint16_t）

Point 4：循环展开

这一步是前三步的补充，主要是利用编译器再尝试优化一下。

简单理解循环展开 (unroll loop) 就是增大 for 循环的步长，让每一个迭代可以多处理一些数据，给编译器提供了更多调度的空间（比如指令重排，寄存器重命名，寄存器复用等）, 同时也减少了分支判断的次数，从而提升性能。操作很简单，示例代码如下：

// 示例代码 4
constexpr step = 128/sizeof(float); // NEON 指令是固定长度 128bit, 一条 NEON 指令可以并行处理 step 个 float, 这里 step=4
flaot32x4_t vload[3]; // 暂存 load 的结果，用于向量化计算
float32x4_t k[3];

k[0] = vdupq_n_f32(kernel_x[0]); // k[0] = {0.25, 0.25, 0.25}
k[1] = vdupq_n_f32(kernel_x[1]); // k[1] = {0.5, 0.5, 0.5}
int j = 1;
for(int i = 0; i < ksize-1; ++i){
    for(; j < w - 1 - step * 2; j += step * 2){
        vload[0] = vld1q_f32(src[i][j-1]);
        vload[1] = vld1q_f32(src[i][j]);
        vload[2] = vld1q_f32(src[i][j+1]);
        float32x4_t tmp0 = vmulq_f32(vload[1], k[1]);
        float32x4_t vbuf0 = vmlaq_f32(tmp0, k[0], vaddq_f32(vload[0], vload[2]));
        vst1q_f32(buf[i][j], vbuf0);

        vload[0] = vld1q_f32(src[i][j + step - 1]);
        vload[1] = vld1q_f32(src[i][j + step]);
        vload[2] = vld1q_f32(src[i][j + step + 1]);
        float32x4_t tmp1 = vmulq_f32(vload[1], k[1]);
        float32x4_t vbuf1 = vmlaq_f32(tmp1, k[0], vaddq_f32(vload[0], vload[2]));
        vst1q_f32(buf[i][j + step], vbuf1);
    }
    // 处理剩下的部分数据
    for(; j < w-1 ; ++j ){
        buf[i][j] = (src[i][j-1] + src[i][j+1]) * kx[0] + src[i][j] * kx[1];
    }
}

稍微总结一下： unroll 次数需要根据实际情况分析测试，也可以尝试不同的 unroll 次数，进行搜索确认。

Point 5：考虑减少重复访存

前面 4 步完成了计算的优化，还需要考虑访存的优化，同样是考虑减少重复的访存。

观察一下示例代码 3，它的三次 vld1q_f32 分别 load 了

vload[0] : { src[0][j-1] , src[0][j] , src[0][j+1] , src[0][j+2] }
vload[1] : { src[0][j] , src[0][j+1] , src[0][j+2] , src[0][j+3]　 }
vload[2] : { src[0][j+1] , src[0][j+2] , src[0][j+3] , src[0][j+4] }
三个向量。下一个 iter 又 load 了
vload[0] : { src[0][j+3] , src[0][j+4] , src[0][j+5] , src[0][j+6] }
vload[1] : { src[0][j+4] , src[0][j+5] , src[0][j+6] , src[0][j+7] }
vload[2] : { src[0][j+5] , src[0][j+7] , src[0][j+8] , src[0][j+9] }

可以发现 src[0][j+3] 这个位置被重复 load 了 3 次。于是考虑引入一组向量 head, body, tail 去减少重复访存。示例代码如下：

// 示例代码 5
constexpr step = 128/sizeof(float); // NEON 指令是固定长度 128bit, 一条 NEON 指令可以并行处理 step 个 float
flaot32x4_t vload[3]; // 暂存 load 的结果，用于向量化计算
float32x4_t k[3];

k[0] = vdupq_n_f32(kernel_x[0]); // k[0] = {0.25, 0.25, 0.25}
k[1] = vdupq_n_f32(kernel_x[1]); // k[1] = {0.5, 0.5, 0.5}

for(int i = 0 ; i < ksize - 1; i++){
    float32x4_t head, body, tail; // 每处理一行时，定义一组变量 head, body, tail 去存 load 的结果，通过 vextq 指令去拼凑出和之前三次 vld1q 等效的向量，即上边的 fa[0], vload[1], vload[2]
    body = vld1q_f32(src[i][1]);
    tail = vld1q_f32(src[i][1]);
    int j = 0;
    for(; j < w - 1 - step; j += step){
        head = body;
        body = tail;
        tail = vld1q_f32(src[i][j+step]);

        vload[0] = vextq_f32(head, body, 3); // vextq_f32 用来拼凑向量，假设 head = {0,1,2,3}, body= {4,5,6,7} , 则 vload[0] = {3,4,5,6}
        vload[1] = body;                     // vload[1] = {4,5,6,7}
        vload[2] = vextq_f32(body, tail, 1); // vextq_f32 用来拼凑向量，假设 body = {4,5,6,7}, tail = {8,9,10,11}, 则 vload[2] = {5,6,7,8}
        float32x4_t tmp = vmulq_f32(vload[1], k[1]);
        float32x4_t vbuf = vmlaq_f32(tmp, k[0], vaddq_f32(vload[0], vload[2]));
        vst1q_f32(buf[i][j], vbuf);
    }
    // 处理剩下的部分数据
    for(; j < w - 1; ++j ){
        buf[i][j] = (src[i][j-1] + src[i][j+1]) * kx[0] + src[i][j] * kx[1];
    }
}

通过这种方式，原先每个for(; j < width - 1 - step; j += step)循环里需要 3 次 vld1q，现在只需要 1 次。代价是多了一些赋值和 vextq 的拼凑指令。

简单总结一下： 当算子是 memory-bound 时，可以考虑减少访存次数。比如：设计数据结构去缓存访存结果，减少重复访存。

那么就引出如下的两个问题：

Q1 : 如何知道算子是 bound 在计算上还是访存上？

可以借助 roofline model 进行分析。roofline model 主要是回答“在算力峰值为 A, 带宽峰值为 B 的设备上，跑计算量为 C, 访存量为 D 的程序能达到性能峰值 E 是多少”。具体可以参考引用 ³ 的论文。

Q2 : 如何知道设备的算力峰值和带宽峰值？

测设备的算力峰值和带宽峰值主要是通过 macro-benchmark。在 github 上可以找到一些 macro-benchmark 的 repo，比如 stream、lmbench 等

Point 6：增加多线程计算

当计算和访存都优化完，保证计算和访存都是必要且最少的，之后考虑引入多线程。

在示例代码 2 中，可以把整个 height 拆成若干段，每一段执行相同的代码，这样就可以开多个线程去并行处理。

Point 7：汇编优化

前 6 步属于 C++/instrinsic 层面的粗调，这一步是汇编层面的优化，属于微调，性能优化应该遵循 “先粗调再细调” 的原则。当在 C++层面想不到其它优化点时，可以考虑进行汇编优化。这里简单介绍一下，不过多展开。主要有以下要点：

使用 asm 语法 ⁴，内嵌一段汇编，替换原先的 C++代码，并保证精度正确
结合 compiler explorer⁵ , 读懂每条汇编指令 ⁶ 的意思
寻找一些多余指令，比如通过寄存器重命名或者指令重排，复用中间结果，从而减少一些指令
先去掉所有的访存指令，保留核心计算指令。通过指令重排等手段，让 GFLOPS 尽量达到峰值的 90%以上。
通过多发射，用计算尽可能去掩盖访存。

需要注意的是:

另外针对不同的平台，会有不同的优化技巧，需要结合体系架构相关的信息去做针对性的优化。

用汇编优化也是因为顺序执行核心对指令顺序很敏感，编译器的重排不能保证最优且容易受编译器版本影响。

例子 1：通过查阅 cortex-a55 的优化指南 ⁷，可以得到如下信息：

cortex-a55 是一个双发射（有两个发射端口，一个 cycle 可以发射两条指令，有两套硬件单元可以同时执行），顺序执行的核心。
不同指令的执行 latency , 执行 throughput, 允许发射的端口号等信息。比如

这里的 LDR 指令 (D-form) 负责从指定地址 load 64bit 的数据到寄存器里

* exec latency 为 3 ： 它的执行需要 3 个 cycle 
* exec throughput 为 1 ： 一个 cycle 只能发射一条 LDR 指令
* Dual-issue 编号为 11 : 可以从 slot0 或者 slot1 发射出去。

知道这些信息，我们可以通过选择可以双发射的指令组合，达到掩盖部分指令的开销的目的。比如

LDR 指令 (D-form) 可以从 slot0 或 slot1 发射出去，
LDR 指令（Q-form）只能从 slot 0 发射出去， FADD 指令 (Q-form) 也只能从 slot 0 发射出去。

于是可以用 LDR（D-form）替换 LDR(Q-form)，去和 FADD(Q-form) 做双发射，从而掩盖了 LDR 指令的开销。

Note :

Q-form 指令一次操作 128bit 的数据

D-form 指令一次操作 64bit 的数据

// 示例代码 6
// 原汇编
“fmla v1.4s, v1.4s, v1.s[0]\n”
“ldr q0, [%[b_ptr]]\n”
“fmla v2.4s, v2.4s, v2.s[0]\n”
“fmla v3.4s, v3.4s, v3.s[0]\n”
“fmla v4.4s, v4.4s, v4.s[0]\n”
“fmla v5.4s, v5.4s, v5.s[0]\n”
“fmla v6.4s, v6.4s, v6.s[0]\n”
/*
 * ldr q0, [%[b_ptr]] 是 从 ptr 加载 16B 到 v0 寄存器
 */
 
// 优化后的汇编
“fmla v1.4s, v1.4s, v1.s[0]\n”
“ldr d0, [%[b_ptr]]\n”
“fmla v2.4s, v2.4s, v2.s[0]\n”
“ldr x0, [%[b_ptr], #8]\n”
“fmla v3.4s, v3.4s, v3.s[0]\n”
“fmla v4.4s, v4.4s, v4.s[0]\n”
“fmla v5.4s, v5.4s, v5.s[0]\n”
“ins v0.d[1], x0\n”
“fmla v6.4s, v6.4s, v6.s[0]\n”
/*
 * ldr d0, [%[b_ptr]] 是从 b_ptr 加载 8B 到 v0 寄存器的低 8B
 * ldr x0, [%[b_ptr], #8] 是从 b_ptr+8 加载 8B 到 x0 寄存器
 * ins v0.d[1], x0 是从 x0 寄存器加载 8B 到 v0 寄存器的高 8B
 */

例子 2: 查阅 cortex-a55 的优化指南 ^7:1，可以知道 fmla,fmul,fadd 指令 (Q-form) 的 latency 都是 4 个 cycle，throughput 都是 1 个 cycle，发射端口都是 0, 于是用 fmla 去替换 fadd+fmul 就可以减少一条指令。

例子 3： cortex-a7 是一个单发射，顺序执行的核心。那么主要是考虑根据指令的 latency，进行指令重排，尽可能排满流水。

其他可能的优化点

完成上述优化步骤后，如果性能还不达标，可以再考虑如下几点优化。

调整内存布局

这里至少涉及两个方面。一方面是内存地址的对齐，不同硬件设备都有一些地址对齐的要求，比如 ARM AArch64 Load/Store 指令要求访问的地址和所访问元素的大小（比如 4 字节）对齐，不然可能会触发对齐错误，带来额外的性能损失。另一方面是内存布局，比如 NHCW,NCHW 等，对于同一段代码，不同的内存布局，访存的连续性是不一样的。也会有自定义的内存布局，在一些情况下可以取得不错的优化效果。

良好的 C++代码

C++的写法可以多关注内联，引用，移动语义等，函数接口参数尽可能使用简单的数据结构，可以提升程序性能，减少不必要的开销。

把一些函数形参放到模板参数里

这样的做法可以让编译器在编译链接时进行一些简单的运算，提前知道一些参数信息也有助于编译器的优化。比如可以把一些 if 判断的 flag 抽离，做为模板参数。

优化思路总结

上述通过 GaussianBlur 的例子，介绍了一些可能的优化点，但这只是整个优化流程的一个步骤。

性能优化是一个不断迭代的过程，很难追求一步到位。一般的优化流程可以用下图表示：

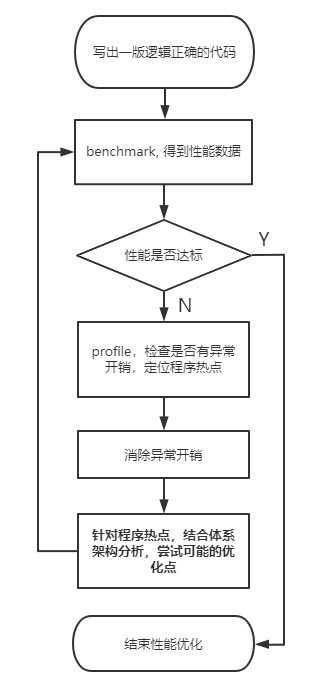
benchmark

为了得到一个正确的优化反馈，需要做科学严谨地 benchmark。笔者认为 benchmark 至少需要考虑以下因素：

跑多次取平均值
跑多次之前，需要先额外跑几次，做 warm up。目的是将数据加载到 cache 中，使得后续测速速度相对稳定
做速度对比时，需要保证两边的各种可能影响速度的要素尽可能对齐，包括：
- 输入地址是否都做了地址对齐
- 关键的编译选项是否对齐
- 依赖的第三方库版本是否对齐
- 编译工具链是否对齐
- 算子的各种参数组合对齐等等
观察每个 iter 的速度数据，如果波动较大，则应该舍去，重新测速
设置 cpu 亲和度，进行绑核

也可以考虑使用 google_benchmark 等 benchmark 工具。

profile

做性能优化之前，往往需要先做一下 profile，了解程序的热点（耗时最多的地方），观察有没有异常的开销（比如函数封装的 overhead 过大）。

可以使用一些 profiling 工具，硬件厂商通常会提供自己的 profiling 工具，比如 x86 上用 intel 的 vtune，nvidia 用上 nsight compute，arm 上用 arm map, android 上用 simple_perf 等。

也可以手动加计时函数，比较核心代码的速度和封装后的速度，确定封装带来的 overhead 是否合理。

参考文献

高斯模糊 https://zh.wikipedia.org/wiki/%E9%AB%98%E6%96%AF%E6%A8%A1%E7%B3%8A ↩︎
Stack Blur https://medium.com/mobile-app-development-publication/blurring-image-algorithm-example-in-android-cec81911cd5e ↩︎
roofline model https://people.eecs.berkeley.edu/~kubitron/cs252/handouts/papers/RooflineVyNoYellow.pdf ↩︎
C++内嵌汇编 https://dmalcolm.fedorapeople.org/gcc/2015-08-31/rst-experiment/how-to-use-inline-assembly-language-in-c-code.html#outputoperands ↩︎
compiler explorer https://godbolt.org/ ↩︎
arm 汇编指令详细介绍 https://developer.arm.com/documentation/ddi0487/ha/?lang=en ↩︎
Arm Cortex-A55 Software Optimization Guide https://developer.arm.com/documentation/EPM128372/0300/?lang=en ↩︎ ↩︎

前言