MegEngine 实现线性回归¶
本教程涉及的内容
理解机器学习中数据(Data)和数据集(Dataset)有关的概念,用 MegEngine 进行封装;
理解小批量梯度下降(Mini-batch Gradient Descent),以及
DataLoader的基础使用;根据前面的介绍,使用 MegEngine 完成加利福尼亚住房数据集的房价预测任务。
本教程中将接触到更多 Tensor 操作与运算的接口
需要用到一些线性代数知识,下面这些材料用于在阅读教程感到吃力时,进行回顾:
Kaare Brandt Petersen - The Matrix Cookbook
3Blue1Brown - 线性代数的本质 [Bilibili] / Essence of linear algebra [YouTube]
在 1.7 版更改: 本教程中所用的数据集已经由波士顿住房数据集替换成加利福尼亚住房数据集。
获取原始数据集¶
在上一个教程《 MegEngine 基础概念 》 中,我们尝试用 MegEngine 去拟合一条直线。 但在现实世界中,我们所面临的任务可能没有这么简单,数据的表示也不是这么直接的抽象。 因此在这个教程中,我们将更完成一个更加复杂的线性回归任务,将用到 加利福尼亚住房数据集 , 完成房价预测任务。
我们将使用到 Scikit-learn (请自行安装)中的接口来获取加利福尼亚住房数据:
from sklearn.datasets import fetch_california_housing
from os.path import expanduser
DATA_PATH = expanduser("~/data/datasets/california")
X, y = fetch_california_housing(data_home=DATA_PATH, return_X_y=True)
注:数据集将从 StatLib 获取,请确保能正常访问该网站。
得到的 X 和 y 将会是 NumPy 的 ndarray 格式。
社区中有许多公开的数据集供我们学习和研究使用,因此许多 Python 库中会封装好获取一些数据集的接口,方便用户调用。
我们在后续的教程中还会看到 MegEngine 中提供的 data.dataset 模块,提供了类似的功能。
>>> print(X.shape, y.shape)
(20640, 8) (20640,)
了解数据集信息¶
回忆一下,在上一个教程中,我们的输入数据形状为 \((100, )\), 表示共有 100 个样本, 每个样本只含有一个自变量,因此也叫一元线性回归; 而此处得到的 \(X\) 的形状为 \((20640, 8)\), 表明共有 20640 个样本,后面的 8 意味着什么呢? 很容易联想到,这里存在着 8 个自变量,即我们将用多元线性回归模型来完成房价预测。
California Housing 数据集
查阅 California Housing dataset 文档可知: 加州住房数据集中一共有 20640 个示例(Instances),每个示例包括 8 个属性(Attributes)。 其中属性信息如下:
MedInc: median income in block groupHouseAge: median house age in block groupAveRooms: average number of rooms per householdAveBedrms: average number of bedrooms per householdPopulation: block group populationAveOccup: average number of household membersLatitude: block group latitudeLongitude: block group longitude
每个属性都用一个具体数值进行了表示,而且告知我们没有缺失的属性值。
本教程中刻意缺失的流程
有过机器学习或数据挖掘项目经验的用户可能知道, 通常我们会对拿到的原始数据进行探索性数据分析(Exploratory Data Analysis,EDA), 帮助我们后期更好地进行特征工程和选择模型。感兴趣的读者可以自行了解, 但这些步骤不是本教程中关注的重点,介绍这些流程反而会加大学习难度。
数据的相关概念¶
我们已经初步了解了加利福尼亚住房数据集的相关信息,接下来可以探讨数据(Data)的相关概念。
想要让计算机帮助我们解决现实问题,就需要对问题进行建模,抽象成计算机容易理解的形式。 我们已经知道机器学习是通过数据进行学习的(Learning from data),因此数据的表征很关键。 我们在描述一个事物的时候,通常会寻找其属性(Attribute)或者说特征(Feature):
比如我们描述一只柴犬的长相,会说这只柴的鼻子如何、耳朵如何、毛发如何等等;
又比如在电子游戏中,角色的属性经常有生命值、魔法值、攻击力、防御力等属性;
在计算机中,这些信息都需要用离散数据进行表示,最常见的做法就是量化成数值。
弃用波士顿房屋数据集的原因 - 机器学习的伦理问题
我们在旧的教程中使用了波士顿房屋数据集来完成房价预测任务,但现在已经被弃用。 如《 racist data destruction? 》 一文中的调查,该数据集的作者设计了一个不可逆变量“B”,假设种族隔离对房价有积极影响。 这样的数据集是存在伦理道德争议的,因此不应当被广泛使用。
尽管换用了数据集,但本教程中关注的重点不是数据特征的选取是否科学,关心的是特征数量变多的这一情况:
>>> X[0] # a sample
array([ 8.3252 , 41. , 6.98412698, 1.02380952,
1. , 2.55555556, 37.88 , -122.23 ])
住房数据集的中的每个示例我们也称之为样本(Sample),因此样本容量 \(n\) 为 20640. 每个样本中记录的属性信息可以用一个特征向量 \(\boldsymbol{x}=\left(x_{1}, x_{2}, \ldots, x_{d}\right)\) 来表示, 里面的每个元素对应着该样本的某一维特征,我们将特征的维数简记为 \(d\), 其值为 8. 因此我们的数据集可以用一个数据矩阵 \(X\) 来表示,预测目标又叫做标记(Label):
其中 \(x_{i,j}\) 表示第 \(i\) 个样本的第 \(j\) 维特征, 标量 \(y_i\) 为样本 \(\boldsymbol{x}_{i}\) 对应的标记值, \((\boldsymbol{x}, y)\) 组成了样例(Example)。 在进行矩阵运算时,向量默认是列向量
计算:乘法形式的讨论¶
我们任务是用线性回归模型 \(Y=X \beta+\varepsilon\) 来预测房价,其中 \(\varepsilon\) 是随机扰动。 与一元线性回归的区别在于,此时的自变量 \(x\) 有多个,我们的参数 \(\boldsymbol{w}\) 也由标量变成了向量, 对单个样本 \(\boldsymbol{x}\) 有:
两个向量点积将得到一个标量,与标量 \(b\) 相加后得到的值就是预测的房价。
在 MegEngine 中,向量点积操作的接口是 functional.dot:
import megengine
import megengine.functional as F
n, d = X.shape
x = megengine.Tensor(X[0])
w = F.zeros((d, ))
b = 0.0
y = F.dot(w, x) + b
>>> print(y, y.shape)
Tensor(0.0, device=xpux:0) ()
为了利用向量化的特性(避免写出 for 循环),我们希望对整批数据 \(X\) 有:
NumPy 中的 numpy.dot 接口的确支持 n 维数组与 1 维数组(向量)之间的点乘:
import numpy as np
w = np.zeros((d,))
b = 0.0
y = np.dot(X, w) + b
>>> y.shape
(20640,)
MegEngine 中的 dot 不支持矩阵与向量相乘
阅读 numpy.dot 的 API 文档会发现,其支持各种不同输入形式的点积操作。
如果输入 \(a\) 和 \(b\) 都是 1 维数组(向量),等同于内积
numpy.inner;如果输入 \(a\) 和 \(b\) 都是 2 维数组(矩阵), 等同于矩阵乘法
numpy.matmul或中缀运算符@;如果输入 \(a\) 和 \(b\) 中有一个是 0 维数组(标量), 等同于元素乘法
numpy.multiply或中缀运算符*;如果输入 \(a\) 是 n 维数组,输入 \(b\) 是 1 维数组, 则会在 \(a\) 的最后一轴与 \(b\) 计算和积;
如果…
可见这个 numpy.dot 接口有些过于全能了,用户如果不查阅文档,
很难想到调用它时的具体行为,这与 MegEngine 的接口设计哲学不符合。
MegEngine 中强调语法透明、行为显式,尽量避免存、歧义和误用,
因此 functional.dot 专指向量点积,不支持其它形状的输入。
这也意味着,同名或者相似命名的接口不代表完全一样的定义实现逻辑。 我们还可以参考 MARLAB 中的 Dot product 会发现定义也不和 NumPy 完全一样。
在 MegEngine 中矩阵乘法的接口为 functional.matmul, 对应中缀运算符 @.
Python 官方提案 PEP 465
提供了矩阵乘法的专用中缀运算符 @ 相关讨论和推荐语义,兼容不同形状的输入形式。
里面提到了,对于 1 维向量输入,可以通过附加一个长度为 1 的维度而提升为 2 维矩阵,
执行矩阵乘法操作后,再从输入出删除临时添加的维度。这样就使得 矩阵@向量
和 向量@矩阵 都变成了合法操作(假定形状兼容),且都返回一维向量。
以本次多元线性回归模型为例,其计算方式在 MegEngine 中就变成了 \(Y=XW+B\):
>>> X = megengine.Tensor(X)
>>> W = F.expand_dims(F.zeros(d, ), 1)
>>> b = 0.0
>>> y = F.squeeze(F.matmul(X, W) + b)
>>> y.shape
(20640,)
通过
expand_dims接口,我们将形状为 \((d,)\) 的零向量 \(w\) 变成了形状为 \((d,1)\) 的列向量 \(W\);通过
matmul接口,执行矩阵乘法 \(P=XW\), \(P\) 为中间计算结果;执行 \(Y=P+b\) 时,标量 \(b\) 广播称为形状兼容的列向量 \(B\);
通过
squeeze接口,去掉了冗余的维度,将 \(Y\) 变回了向量 \(y\).
尽管 expand_dims 和 squeeze 的功能也可以通过 reshape 来实现,
但是为了代码的可读性,在存在专用接口的情况下,我们应当尽可能地使用这些具有透明语义的接口。
由于存在着 PEP 465 的推荐定义,因此 MegEngine 的 matmul 也兼容非矩阵形式的输入:
>>> X = megengine.Tensor(X)
>>> w = F.zeros((d,))
>>> y = F.matmul(X, w) + b
>>> y.shape
(20640,)
为什么 matmul 兼容不同类型的形状
对不同输入形状进行兼容,会使得在高维情况下的局部矩阵乘法代码非常好写,且不影响代码可读性。
尽管这可能与 MegEngine 接口设计哲学有些冲突,但兼容社区一致标准是最低要求。
矩阵乘法的表示在 Python 数据科学社区中已经经过长期的广泛讨论和实践验证,最终达成了共识。
这是 Python 语言层面提供的官方参考,而 NumPy 中 numpy.dot 接口设计并没获得社区的一致承认。
现在我们已经实现了一份足够向量化的代码,看来可以使用梯度下降算法来优化模型参数了。
梯度下降的几种形式¶
如果对于每个输入的样本,我们都及时地计算损失并且更新模型参数,参数迭代频率会非常高 —— 这种做法叫随机梯度下降(Stochastic Gradient Descent, SGD), 也被叫做在线梯度下降(Online Gradient Descent),这种形式的梯度下降非常容易理解。 问题在于,频繁的更新会导致梯度的变化比较跳跃(方向不稳定); 另外,在整个训练过程中需要进行多次的循环运算,如果数据规模变得巨大,这种计算形式将变得十分低效。
我们在教程中已经多次强调了:要用向量化形式代替 for 循环形式的写法,来追求更高的计算效率。 因此我们在前向计算时,通常会选择将批数据作为输入,而不是单个样本,这其实是并行计算的思想。 除此原因外,批梯度下降还能减少异常数据带来的干扰,朝着整体更优的方向去迭代参数,损失更稳定地收敛。
但批梯度下降也存在自身的局限性。过于稳定的梯度变化可能会导致模型过早地收敛到一组不太理想的参数。 我们对于梯度进行累加的策略也有可能引入了其它的不确定因素,影响了整个训练过程。 考虑大规模的数据输入情况,此时我们很有可能无法将整个数据集一次性加载到内存中; 即便解决了内存容量问题,在大型数据集上进行批梯度下降,参数迭代更新的速度会显著变慢。
容易被忽视的是将 NumPy ndarray 转换成 MegEngine Tensor 的过程,这里其实也存在着数据搬运:
>>> X = megengine.Tensor(X)
权衡取舍随机梯度下降和批梯度下降之间的优缺点,我们得到了梯度下降的另一变体:小批量梯度下降。
小批量梯度下降¶
小批量梯度下降(Mini-Batch Gradient Descent)在训练时会将数据集划分成多个小的分批数据, 在每批数据上计算平均损失和梯度以减少方差,然后更新模型中的参数。 它的好处是参数的迭代频率高于批量梯度下降,有助于在损失收敛时避开局部最小值; 可以控制每次加载多少数据到内存,兼顾了计算效率以及参数更新频率。
在深度学习领域,梯度下降通常指代的是小批量梯度下降。
问题在于,采用小批量梯度下降算法将引入另一个超参数 batch_size, 表示每一批数据的规模大小。

梯度下降过程中,损失变化的等高线图,箭头表示梯度下降的方向。¶
当
batch_size为 1 时,等同于随机梯度下降;当
batch_size为 n 时,等同于批梯度下降。
通常我们会根据硬件架构(CPU/GPU)来决定 batch_size 值的大小,比如会设置成如 32, 64, 128 等 2 的幂。
如何获取分批数据¶
在 MegEngine 中提供了 megengine.data 模块, 里面提供我们想要的数据分批功能,示范代码如下:
from megengine.data import DataLoader
from megengine.data.dataset import ArrayDataset
from megengine.data.sampler import SequentialSampler
from os.path import expanduser
DATA_PATH = expanduser("~/data/datasets/california")
X, y = fetch_california_housing(DATA_PATH, return_X_y=True)
house_dataset = ArrayDataset(X, y)
sampler = SequentialSampler(house_dataset, batch_size=64)
dataloader = DataLoader(house_dataset, sampler=sampler)
for batch_data, batch_label in dataloader:
print(batch_data.shape)
break
在上面的代码中,我们用 ArrayDataset 对 NumPy ndarray 格式的数据集进行了快速封装,
接着使用顺序采样器 SequentialSampler 对 house_dataset 进行了采样,
二者用来作为参数初始化 DataLoader,
最终获取到了一个可迭代的对象,每次提供 batch_size 大小的数据和标记。
>>> len(dataloader)
323
我们在上面选定的 batch_size 为 64,样本容量为 20640, 因此可以划分成 323 批数据。
注解
我们这里的介绍有些简略,但不影响本教程的学习,目前只需要了解大概作用即可;
如果你对背后的原理感兴趣,可以阅读 使用 Data 构建输入 Pipeline 中的详细介绍。
再次思考优化目标¶
我们在上一个教程提到了优化目标,给出了 “犯错越少,表现越好” 的核心原则, 并选择了整体平均损失(预测值和真实值之间的误差函数)作为优化目标, 最终通过损失值是否下降以及直接观察直线的拟合程度来判断模型性能的好坏。 但仔细思考一下,我们的真实意图并不仅仅是希望我们的模型在 已知的 这些数据集上表现良好。
警惕过拟合现象¶
我们更加希望我们的模型具有比较好的泛化(Generalization)能力, 在面对 全新的、从未见过的 数据时,也能进行准确的预测。 如果单纯地去基于已经观测到的这些数据进行求解, 对于线性回归模型 \(\hat{y} = \theta^{T} \cdot \boldsymbol{x}\), 我们其实完全可以基于样本 \(X\) 和标记 \(\boldsymbol{y}\) 求得一个解析解 \(\theta = (X^{T}X)^{-1}X^{T}\boldsymbol{y}\). 这个结果也可以从概率模型视角用极大然估计(Maximum Likelihood Estimation)求得 —— 利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。 (本教程不需要知道详细的推导和证明过程,感兴趣的读者可以查看 CS229 课程讲义 )
过拟合指的是我们的模型在已知数据集上训练表现良好,在新样本上预测却表现不佳的情况。 如果一个模型仅仅在用于训练的数据上表现良好甚至是优异,但却在实际应用时表现不佳… 尴尬,这表明我们训练出的模型已经过拟合。导致过拟合的原因有很多, 比如训练样本数量过少,在当前模型上训练轮数(Epochs)过多等等。 对应的解决方法有很多,比如使用更大规模的训练数据集、使用更复杂的模型等等…
本教程中介绍的一种防止过拟合的做法是,将数据集进行划分,并及时评估模型性能。
划分数据集¶
数据集的常见划分方式
训练集(Training dataset):用来进行训练并且优化模型参数的数据集;
验证集(Validation dataset):用来在训练过程中及时评估模型性能的数据集;
测试集(Test dataset):模型训练完成后,最终对模型预测能力进行测试的数据集;
验证集有时候也被叫做开发集(Develop dataset), 它本身虽然在训练模型的过程中被用于做及时验证, 但仅用于计算损失,不会参与到反向传播和参数优化的流程中去。 如果在训练过程中发现训练集上的损失在降低,而验证集上的损失在上升, 则表示发生了过拟合现象。
验证集还能够帮助我们调整除 Epoch 外的超参数,但具体做法不会在本教程中介绍。
一些公开数据集会为使用者划分好训练集与测试集(我们在后面的教程会看到), 测试集在最终用做模型性能测试前,要被看作是 “从未见过的”、“无法使用的” 数据。
方便起见,我们使用 Scikit-learn 中提供的接口对住房数据集进行划分:
from sklearn.model_selection import train_test_split
X, y = fetch_california_housing(DATA_PATH, return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=37)
>>> print(X_train.shape, y_train.shape) # Temporary
>>> print(X_test.shape, y_test.shape)
(16512, 8) (16512,)
(4128, 8) (4128,)
从原始的数据集中,我们取出了 80% 作为训练集,20% 作为测试集。
接下来我们需要进一步从训练集中划分出其 25% 作为验证集:
>>> X_train, X_val, y_train, y_val = train_test_split(X_train, y_train,
... test_size=0.25, random_state=37)
>>> print(X_train.shape, y_train.shape)
>>> print(X_val.shape, y_val.shape)
(12384, 8) (12384,)
(4128, 8) (4128,)
最终,我们划分出的训练集:验证集:测试集的占整体数据集比例为 3:1:1.
练习:多元线性回归¶
准备训练集、验证集和测试集对应的 ArrayDataset, Sampler 以及 DataLoader.
通常在训练模型时,我们会选择打乱训练集样本的顺序,但由于我们在划分数据集时调用的接口已经执行了乱序操作,
这里我们直接选择使用顺序采样器,并将批块大小设置成 128.(这个超参数你可以自己调整)
数据预处理与归一化(高亮行)
注意在下面的代码中,我们用到了 data.transform 模块,
该模块帮助我们在将数据加载时进行一些预处理(Preprocessing)变化操作,
比如归一化 Normalize —— 通过计算训练集中样本的相关统计数据,对每个特征独立地进行归一化。
这样做的好处之一是优化器的学习率不用再根据输入数据的数值范围进行调整,通常可以从 0.01 开始。
且大多数机器学习算法会要求特征具有 0 均值和单位方差,否则可能表现不佳。
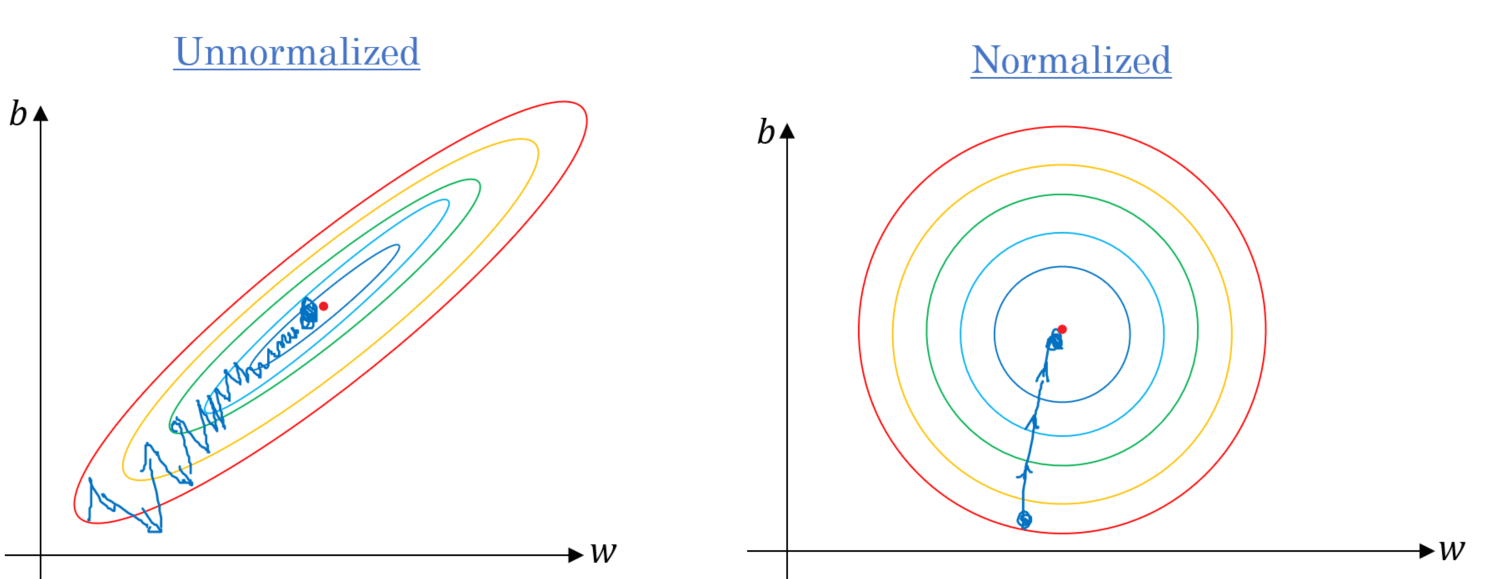
数据归一化后,其损失变化等高线图也更加均匀,在进行梯度下降时,通常能够更快地收敛。¶
我们在上一个教程中随机生成数据时刻意地符合均匀分布,因此无需进行归一化预处理。
我们在后续的教程中会看到更多的数据预处理操作,预处理操作有不同的类型和意义, 感兴趣的读者可以提前查阅 MegEngine 文档等材料,目前只需要对此留有一个基本印象即可。
import megengine.data.transform as T
transform = T.Normalize(mean=X_train.mean(), std=X_train.std()) # Preprocessing
train_dataset = ArrayDataset(X_train, y_train)
train_sampler = SequentialSampler(train_dataset, batch_size=128)
train_dataloader = DataLoader(train_dataset, train_sampler, transform)
val_dataset = ArrayDataset(X_val, y_val)
val_sampler = SequentialSampler(val_dataset, batch_size=128)
val_dataloader = DataLoader(val_dataset, val_sampler, transform)
test_dataset = ArrayDataset(X_test, y_test)
test_sampler = SequentialSampler(test_dataset, batch_size=128)
test_dataloader = DataLoader(test_dataset, test_sampler, transform)
按照上面演示过的内容,定义我们的线性回归模型,同时准备好 GradManager 与 Optimizer :
import megengine
import megengine.functional as F
import megengine.optimizer as optim
import megengine.autodiff as autodiff
nums_feature = X_train.shape[1]
w = megengine.Parameter(F.zeros((nums_feature,)))
b = megengine.Parameter(0.0)
def linear_model(X):
return F.matmul(X, w) + b
gm = autodiff.GradManager().attach([w, b])
optimizer = optim.SGD([w, b], lr=0.01)
万事俱备,可以开始训练我们的模型了:
Mini-batch 的训练过程是怎样的
回忆一下,如果是批梯度下降算法,每经过一轮(Epoch)训练,参数只会迭代更新一次。
而现在我们使用小批量梯度下降算法,在每一轮训练中,我们会有多个 train_step, 或者说有多个 iter / batch.
每个 Step 都会从 train_dataloader 中读取 batch_size 大小的数据,
执行我们在上个教程已经认识的前向计算、反向计算以及参数更新过程,这时得到的损失是在小批量数据上的平均损失。
根据这个平均损失,对所有的参数计算关于损失的梯度,并进行更新。接着进入下一个 Step, 用下一批数据… 循环往复。
为了及时地观察训练状态,
通常我们每隔一定的 train_step, 就会观察一下当前这批训练数据上损失的变化情况(输出 Log 信息)。
经过一轮完整的训练后,我们会计算在整个训练数据集上的平均损失 training_loss 作为这一轮训练的结果。
然后我们要立即用验证集来评估当前模型的性能,在评估模型性能时,由于只需要进行前向计算和计算损失,
因此可以选用和损失函数(本教程中为 MSE)不同的评估指标,
比如回归任务中可以使用平均绝对误差 MAE, 在 MegEngine 中为 l1_loss 接口。
为了更加严谨地对比,你也可以在训练时每个 Batch 数据计算 MSE, 而完成一轮训练后在整个训练集上使用 MAE 进行评估。
1nums_epoch = 10
2for epoch in range(nums_epoch):
3 training_loss = 0
4 validation_loss = 0
5
6 # Each train step will update parameters once (an iteration)
7 for step, (X, y) in enumerate(train_dataloader):
8 X = megengine.Tensor(X)
9 y = megengine.Tensor(y)
10
11 with gm:
12 pred = linear_model(X)
13 loss = F.nn.square_loss(pred, y)
14 gm.backward(loss)
15 optimizer.step().clear_grad()
16
17 training_loss += loss.item() * len(X)
18
19 if step % 30 == 0:
20 print(f"Epoch = {epoch}, step = {step}, loss = {loss.item()}")
21
22 # Just evaluation the performance in time
23 for X, y in val_dataloader:
24 X = megengine.Tensor(X)
25 y = megengine.Tensor(y)
26
27 pred = linear_model(X)
28 loss = F.nn.l1_loss(y, pred)
29
30 validation_loss += loss.item() * len(X)
31
32 training_loss /= len(X_train)
33 validation_loss /= len(X_val)
34
35 print(f"Epoch = {epoch},"
36 f"training_loss = {training_loss},"
37 f"validation_loss = {validation_loss}")
注意:由于最后一个 Batch 的样本数量 len(X) 可能不足 Batch size 个数,
因此我们在统计损失的总体平均值时,为了严谨性,做法是将每个 Batch 整体损失累加,最后除以总样本数。
如果发现从某一轮训练开始,验证集上的损失持续不断地上升,则有可能发生了过拟合。
最后在测试集上进行真正的测试(和验证集的评估方式应当完全一致):
test_loss = 0
for X, y in test_dataloader:
X = megengine.Tensor(X)
y = megengine.Tensor(y)
pred = linear_model(X)
loss = F.nn.l1_loss(y, pred)
test_loss += loss.item() * len(X)
test_loss /= len(X_test)
print(f"Test_loss = {test_loss}")
在本教程中,如果损失值有收敛的趋势,则表明小批量梯度下降法成功地对线性回归模型完成了优化,我们只关注其有效性,而不关注最终效果。 如果你尝试用最小二乘法去求出本教程中线性回归模型的参数解析解,会发现理想的损失应当能收敛到 0.6 附近。 或许你在调整超参数训练模型的过程中会发现损失值出现 NaN 的情况,亦或者是损失下降到某个值后便不再继续下降,而是在一个区间摆动。 导致这些情况产生的原因有很多,比如学习率过大等等,如果你目前还不能够很好地分析出背后的原因并对症下药。 不用担心,我们会在多次的任务和代码实践中,慢慢地积累经验。
本教程的主要目的是帮助你掌握小批量梯度下降的实现,以及模型训练、验证和测试的完整流程。
参见
本教程的对应源码: examples/beginner/linear-regression.py
总结:初探机器学习¶
让我们再次回顾一下关于机器学习的定义:
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
如果一个计算机程序能够根据经验 E 提升在某类任务 T 上的性能 P, 则我们说程序从经验 E 中进行了学习。
在本教程中,我们的任务 T 是用线性回归模型去预测房价,经验 E 来自于我们的训练数据集, 我们对原始数据集进行了划分,并且在训练集上统计出了均值和方差,方便进行输入数据的归一化预处理。 我们评估模型好坏(性能 P)时有不同的倾向,训练损失使用了 MSE, 而在评估时使用了 MAE. 为了调整超参数 Epoch, 我们划分出了验证集来及时评估模型性能,作为对最终测试的模拟。
机器学习的流程大抵类似:数据获取(标注);数据分析与处理;特征工程;模型选择;优化模型;验证模型性能… 每一个环节又可以衍生出更多的理论知识和实践经验,在初学阶段不必要求自己理解全部,否则容易陷入细节。 线性回归模型可以认为是机器学习领域的 Hello, World! 相信你对此已经有了一个基本的认识。
在下一个教程中,将会接触手写数字的分类任务,并且尝试继续使用线性模型和梯度下降法来完成挑战。
拓展材料¶
数学表示形式之间的区别
你会在不同的数学材料中看到不同的数学记号表示,搞清楚符号定义很关键。
在线性代数中向量一般定义为列向量 \(\vec{x}=\left(x_{1} ; x_{2} ; \ldots x_{n}\right)\), 对于单样本的线性回归有 \(y=\vec{w}^{T} \vec{x}+b\).
在 CS229 中的表示形式是,对于一共有 \(n\) 个样例,特征数量为 \(d\) 的数据集 \((X,\vec{y})\) 有:
其中每个样本 \(x^{(i)} = (x^{(i)}_1;x^{(i)}_2;\ldots ;x^{(i)}_n)\), \(x^{(i)}_j\) 表示第 \(i\) 个样本的第 \(j\) 维特征, \(\theta\) 为参数。
注意到上面的向量用上加箭头 \(\vec{x}\) 的形式来表示,这是因为在板书的过程中, 粗体的 \(\boldsymbol{x}\) 与 \(x\) 很难区分,因此采用了这种形式; 而在印刷体材料中,粗体字还是很容易区分的,因此本教程使用粗体罗马字表示向量。 但我们在使用 Tensor 实际编程时, 标量、向量、列向量和行向量 有实质区别 。
本教程中没有使用上标的形式来表示索引,是因为在我们进行编程实践时, 元素索引均为
X[i][j]这种语法,通常用第一个维度表示样本索引。 各个维度之间没有特殊差异,因此不用上下标进行区分。
关于评估指标
对于回归模型,还有着其它可选的评估指标, 如 RMSE, RMSLE, R Square (R2 score)等, 本教程中只选择了易于理解的 MSE 和 MAE, 感兴趣者可自己去了解一下, 看看换用不同的评估指标,对最终模型的预测性能会有什么样的影响。
Kaggle 机器学习竞赛 - 房价预测
如果我们的任务是给定数据集,要求预测房价(不一定要使用线性回归模型), 则完全可以使用其它的机器学习模型如随机森林等来完成目的, 但本系列 MegEngine 教程并不是一门机器学习课程,因此不会有对各种模型更加详细的介绍。
在 Kaagle 机器学习竞赛平台上提供了本教程中提到的加利福利亚数据集的 修改版本 , 非常适合感兴趣的用户去实验其它的模型和算法(有许多用户分享了自己的方案),可作为拓展练习。