MegEngine 基础概念¶
本教程涉及的内容
介绍 MegEngine 的基本数据结构
Tensor以及functional模块中的基础运算操作;介绍计算图的有关概念,实践深度学习中前向传播、反向传播和参数更新的基本流程;
根据前面的介绍,分别使用 NumPy 和 MegEngine 完成一个简单的直线拟合任务。
学习的过程中应避开完美主义
请以完成教程目标为首要任务进行学习,MegEngine 教程中会充斥着许多的拓展解释和链接,这些内容往往不是必需品。 通常它们是为学有余力的同学,亦或者基础过于薄弱的同学而准备的,如果你遇到一些不是很清楚的地方, 不妨试着先将整个教程看完,代码跑完,再回头补充那些需要的知识。
基础数据结构:张量¶
>>> from numpy import array
>>> from megengine import Tensor
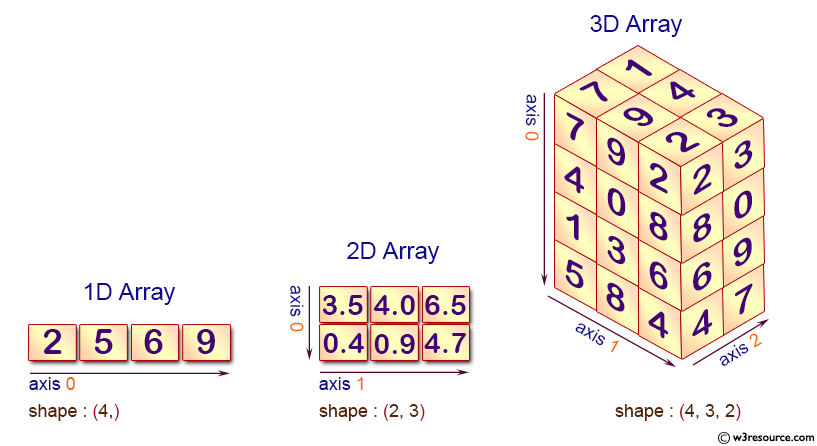
MegEngine 中提供了一种名为 “张量” ( Tensor )的数据结构,
区别于数学中的定义,其概念与 NumPy 1 中的 ndarray 更加相似,即多维数组。
真实世界中的很多非结构化的数据,如文字、图片、音频、视频等,都可以抽象成 Tensor 的形式进行表达。
我们所提到的 Tensor 的概念往往是其它更具体概念的概括(或者说推广):
数学 |
计算机科学 |
几何概念 |
具象化例子 |
|---|---|---|---|
标量(scalar) |
数字(number) |
点 |
得分、概率 |
向量(vector) |
数组(array) |
线 |
列表 |
矩阵(matrix) |
2 维数组(2d-array) |
面 |
Excel 表格 |
3 维张量 |
3 维数组(3d-array) |
体 |
RGB 图片 |
… |
… |
… |
… |
n 维张量 |
n 维数组(nd-array) |
高维空间 |
以一个 2x3 的矩阵(2 维张量)为例,在 MegEngine 中用嵌套的 Python 列表初始化 Tensor:
>>> Tensor([[1, 2, 3], [4, 5, 6]])
Tensor([[1 2 3]
[4 5 6]], dtype=int32, device=xpux:0)
它的基本属性有 Tensor.ndim, Tensor.shape, Tensor.dtype, Tensor.device 等。
我们可以基于 Tensor 数据结构,进行各式各样的科学计算;
Tensor 也是神经网络编程时所用的主要数据结构,网络的输入、输出和转换都使用 Tensor 表示。
注解
与 NumPy 的区别之处在于,MegEngine 还支持利用 GPU 设备进行更加高效的计算。 当 GPU 和 CPU 设备都可用时,MegEngine 将优先使用 GPU 作为默认计算设备,无需用户进行手动设定。 另外 MegEngine 还支持自动微分(Autodiff)等特性,我们将在后续教程适当的环节进行介绍。
如果你完全没有 NumPy 使用经验
可以参考 深入理解 Tensor 数据结构 中的介绍, 或者先查看 NumPy 官网文档和教程;
其它比较不错的补充材料还有 CS231n 的 《 Python Numpy Tutorial (with Jupyter and Colab) 》。
Tensor 操作与计算¶
与 NumPy 的多维数组一样,Tensor 可以用标准算数运算符进行逐元素(Element-wise)的加减乘除等运算:
>>> a = Tensor([[2, 4, 2], [2, 4, 2]])
>>> b = Tensor([[2, 4, 2], [1, 2, 1]])
>>> a + b
Tensor([[4 8 4]
[3 6 3]], dtype=int32, device=xpux:0)
>>> a - b
Tensor([[0 0 0]
[1 2 1]], dtype=int32, device=xpux:0)
>>> a * b
Tensor([[ 4 16 4]
[ 2 8 2]], dtype=int32, device=xpux:0)
>>> a / b
Tensor([[1. 1. 1.]
[2. 2. 2.]], device=xpux:0)
Tensor 类中提供了一些比较常见的方法,比如 Tensor.reshape 方法,
可以用来改变 Tensor 的形状(该操作不会改变 Tensor 元素总数目以及各个元素的值):
>>> a = Tensor([[1, 2, 3], [4, 5, 6]])
>>> b = a.reshape((3, 2))
>>> print(a.shape, b.shape)
(2, 3) (3, 2)
但通常我们会 使用 Functional 操作与计算, 例如使用 functional.reshape 来改变形状:
>>> import megengine.functional as F
>>> b = F.reshape(a, (3, 2))
>>> print(a.shape, b.shape)
(2, 3) (3, 2)
警告
一个常见误区是,初学者会认为调用 a.reshape() 后 a 自身的形状会发生改变。
事实上并非如此,在 MegEngine 中绝大部分操作都不是原地(In-place)操作,
这意味着通常调用这些接口将会返回一个新的 Tensor, 而不会对原本的 Tensor 进行更改。
参见
在 functional 模块中提供了更多的算子(Operator),并按照使用情景对命名空间进行了划分,
目前我们只需要接触这些最基本的算子即可,将来会接触到专门用于神经网络编程的算子。
理解计算图¶
注解
MegEngine 是基于计算图(Computing Graph)的深度神经网络学习框架;
在深度学习领域,任何复杂的深度神经网络模型本质上都可以用一个计算图表示出来。
我们先通过一个简单的数学表达式 \(y=w*x+b\) 作为例子,来介绍计算图的基本概念:
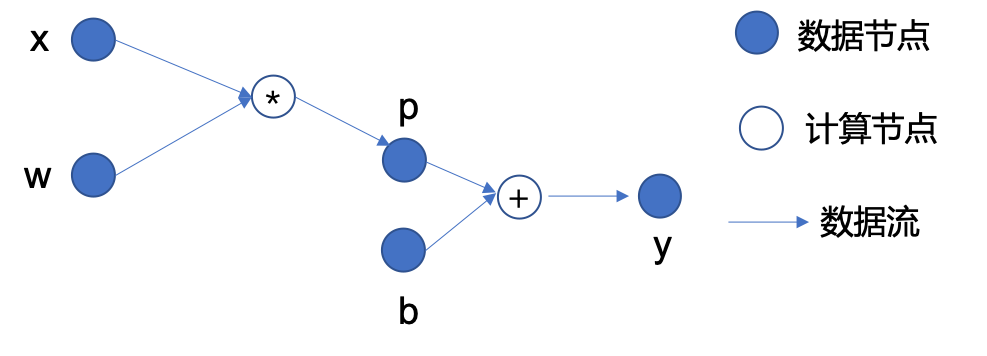
MegEngine 中 Tensor 为数据节点, Operator 为计算节点¶
从输入数据到输出数据之间的节点依赖关系可以构成一张有向无环图(DAG),其中有:
数据节点:如输入数据 \(x\), 参数 \(w\) 和 \(b\), 中间结果 \(p\), 以及最终输出 \(y\);
计算节点:如图中的 \(*\) 和 \(+\) 分别代表乘法和加法两种算子,根据给定的输入计算输出;
有向边:表示了数据的流向,体现了数据节点和计算节点之间的前后依赖关系。
有了计算图这一表示形式,我们可以对前向传播和反向传播的过程有更加直观的理解。
前向传播(Forward propagation)
根据模型的定义进行前向计算得到输出,在上面的例子中即是 ——
输入数据 \(x\) 和参数 \(w\) 经过乘法运算得到中间结果 \(p\);
中间结果 \(p\) 和参数 \(b\) 经过加法运算得到输出结果 \(y\);
对于更加复杂的计算图结构,其前向计算的依赖关系本质上就是一个拓扑排序。
反向传播(Back propagation)
根据需要优化的目标(这里我们简单假定为 \(y\)),通过链式求导法则, 求出模型中所有参数所对应的梯度,在上面的例子中即计算 \(\nabla y(w, b)\), 由偏导 \(\frac{\partial y}{\partial w}\) 和 \(\frac{\partial y}{\partial b}\) 组成。
这一小节会使用到微积分知识,可以借助互联网上的一些资料进行快速学习/复习:
3Blue1Brown - 微积分的本质 [Bilibili] / Essence of calculus [YouTube]
例如,为了得到上图中 \(y\) 关于参数 \(w\) 的偏导,反向传播的过程如下图所示:
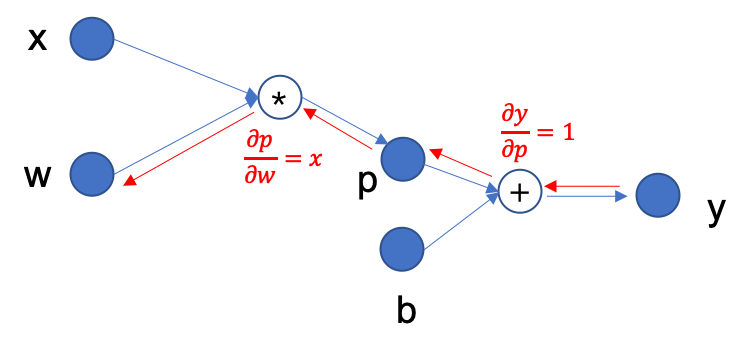
首先有 \(y=p+b\), 因此有 \(\frac{\partial y}{\partial p}=1\);
继续反向传播,有 \(p=w*x\), 因此有 \(\frac{\partial p}{\partial w}=x\);
根据链式法则有 \(\frac{\partial y}{\partial w}=\frac{\partial y}{\partial p} \cdot \frac{\partial p}{\partial w}=1 \cdot x\), 因此最终求出 \(y\) 关于参数 \(w\) 的偏导为 \(x\).
求得的梯度也会是一个 Tensor, 将在下一步参数优化中被使用。
参数优化(Parameter Optimization)
常见的做法是使用梯度下降法对参数进行更新,在上面的例子中即对 \(w\) 和 \(b\) 的值做更新。 我们用一个例子帮助你理解梯度下降的核心思路:假设你现在迷失于一个山谷中,需要寻找有人烟的村庄,我们的目标是最低的平原点 (那儿有人烟的概率是最大的)。采取梯度下降的策略,则要求我们每次都环顾四周,看哪个方向是最陡峭的; 然后沿着梯度的负方向向下迈出一步,循环执行上面的步骤,我们认为这样能更快地下山。
我们每完成一次参数的更新,便说明对参数进行了一次迭代(Iteration),训练模型时往往会有多次迭代。
如果你还不清楚梯度下降能取得什么样的效果,没有关系,本教程末尾会有更加直观的任务实践。 你也可以在互联网上查阅更多解释梯度下降算法的资料。
w, x, b = Tensor(3.), Tensor(2.), Tensor(-1.)
p = w * x
y = p + b
dydp = Tensor(1.)
dpdw = x
dydw= dydp * dpdw
>>> dydw
Tensor(2.0, device=xpux:0)
自动微分与参数优化¶
不难发现,有了链式法则,要做到计算梯度并不困难。但我们上述演示的计算图仅仅是一个非常简单的运算, 当我们使用复杂的模型时,抽象出的计算图结构也会变得更加复杂,如果此时再去手动地根据链式法则计算梯度, 整个过程将变得异常枯燥无聊,而且这对粗心的朋友来说极其不友好,谁也不希望因为某一步算错导致进入漫长的 Debug 阶段。 MegEngine 作为深度学习框架的另一特性是支持了自动微分,即自动地完成反传过程中根据链式法则去推导参数梯度的过程。 与此同时,也提供了方便进行参数优化的相应接口。
Tensor 梯度与梯度管理器¶
在 MegEngine 中,每个 Tensor 都具备 Tensor.grad 这一属性,即梯度(Gradient)的缩写。
>>> print(w.grad, b.grad)
None None
然而上面的用法并不正确,默认情况下 Tensor 计算时不会计算和记录梯度信息。
我们需要用到梯度管理器 GradManager 来完成相关操作:
使用
GradManager.attach来绑定需要计算梯度的参数;使用
with关键字,配合记录整个前向计算的过程,形成计算图;调用
GradManager.backward即可自动进行反向传播(过程中进行了自动微分)。
from megengine.autodiff import GradManager
w, x, b = Tensor(3.), Tensor(2.), Tensor(-1.)
gm = GradManager().attach([w, b])
with gm:
y = w * x + b
gm.backward(y)
这时可以看到参数 \(w\) 和 \(b\) 对应的梯度(前面计算过了 \(\frac{\partial y}{\partial w} = x = 2.0\) ):
>>> w.grad
Tensor(2.0, device=xpux:0)
警告
值得注意的是, GradManager.backward 计算梯度时的做法是累加而不是替换,如果接着执行:
>>> # Note that `w.grad` is `2.0` now, not `None`
>>> with gm:
... y = w * x + b
... gm.backward(y) # w.grad += backward_grad_for_w
>>> w.grad
Tensor(4.0, device=xpux:0)
可以发现此时参数 \(w\) 的梯度是 4 而不是 2, 这是因为新的梯度和旧的梯度进行了累加。
参见
想要了解更多细节,可以参考 Autodiff 基本原理与使用 。
参数(Parameter)¶
你可能注意到了这样一个细节:我们在前面的介绍中,使用参数(Parameter)来称呼 \(w\) 和 \(b\).
因为与输入数据 \(x\) 不同,它们是需要在模型训练过程中被优化更新的变量。
在 MegEngine 中有 Parameter 类专门和 Tensor 进行区分,但它本质上是一种特殊的张量。
因此梯度管理器也支持维护计算过程中 Parameter 的梯度信息。
from megengine import Parameter
x = Tensor(2.)
w, b = Parameter(3.), Parameter(-1.)
gm = GradManager().attach([w, b])
with gm:
y = w * x + b
gm.backward(y)
>>> w
Parameter(3.0, device=xpux:0)
>>> w.grad
Tensor(2.0, device=xpux:0)
优化器(Optimizer)¶
MegEngine 的 optimizer 模块提供了基于各种常见优化策略的优化器,如 SGD 和 Adam 等。
它们的基类是 Optimizer,其中 SGD 对应随机梯度下降算法,也是本教程中将会用到的优化器。
import megengine.optimizer as optim
x = Tensor(2.)
w, b = Parameter(3.), Parameter(-1.)
gm = GradManager().attach([w, b])
optimizer = optim.SGD([w, b], lr=0.01)
with gm:
y = w * x + b
gm.backward(y)
optimizer.step().clear_grad()
调用 Optimizer.step 进行一次参数更新,调用 Optimizer.clear_grad 可以清空 Tensor.grad.
>>> w
Parameter(2.98, device=xpux:0)
许多初学者容易忘记在新一轮的参数更新时清空梯度,导致得到了不正确的结果。
警告
Optimizer 接受的输入类型必须是 Parameter 而非 Tensor, 否则报错。
TypeError: optimizer can only optimize Parameters, but one of the params is ...
参见
想要了解更多细节,可以参考 使用 Optimizer 优化参数 。
优化目标的选取
想要提升模型的预测效果,我们需要有一个合适的优化目标。
但请注意,上面用于举例的表达式仅用于理解计算图, 其输出值 \(y\) 往往并不是实际需要被优化的对象, 它仅仅是模型的输出,单纯地优化这个值没有任何意义。
那么我们要如何去评估一个模型预测性能的好坏呢? 核心原则是: 犯错越少,表现越好。
通常而言,我们需要优化的目标被称为损失(Loss),用来度量模型的输出值和实际结果之间的差异。 如果能够将损失优化到尽可能地低,就意味着模型在当前数据上的预测效果越好。 目前我们可以认为,一个在当前数据集上表现良好的模型,也能够对新输入的数据产生不错的预测效果。
这样的描述或许有些抽象,让我们直接通过实践来进行理解。
练习:拟合一条直线¶
假设你得到了数据集 \(\mathcal{D}=\{ (x_i, y_i) \}\), 其中 \(i \in \{1, \ldots, 100 \}\), 希望将来给出输入 \(x\), 能够预测出合适的 \(y\) 值。
get_point_examples() 源码
下面是随机生成这些数据点的代码实现:
import numpy as np
np.random.seed(20200325)
def get_point_examples(w=5.0, b=2.0, nums_eample=100, noise=5):
x = np.zeros((nums_eample,))
y = np.zeros((nums_eample,))
for i in range(nums_eample):
x[i] = np.random.uniform(-10, 10)
y[i] = w * x[i] + b + np.random.uniform(-noise, noise)
return x, y
可以发现数据点是基于直线 \(y = 5.0 * x + 2.0\) 加上一些随机噪声生成的。
但是在本教程中,我们应当假设自己没有这样的上帝视角, 所能获得的仅仅是这些数据点的坐标,并不知道理想情况下的 \(w=5.0\) 以及 \(b=2.0\), 只能通过已有的数据去迭代更新参数。 通过损失或者其它的手段来判断最终模型的好坏(比如直线的拟合程度), 在后续教程中会向你展示更加科学的做法。
>>> x, y = get_point_examples()
>>> print(x.shape, y.shape)
(100,) (100,)
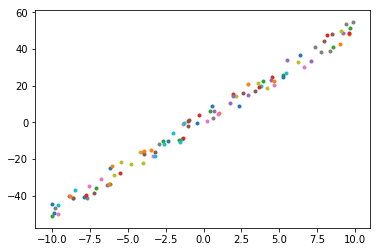
通过可视化分析发现(如上图):这些点的分布很适合用一条直线 \(f(x) = w * x + b\) 去进行拟合。
>>> def f(x):
... return w * x + b
所有的样本点的横坐标 \(x\) 经过我们的模型后会得到一个预测输出 \(\hat{y} = f(x)\).
在本教程中,我们将采取的梯度下降策略是批梯度下降(Batch Gradient Descent), 即每次迭代时都将在所有数据点上进行预测的损失累积起来得到整体损失后求平均,以此作为优化目标去计算梯度和优化参数。 这样的好处是可以避免噪声数据点带来的干扰,每次更新参数时会朝着整体更加均衡的方向去优化。 以及从计算效率角度来看,可以充分利用一种叫做 向量化(Vectorization) 的特性,节约时间(拓展材料中进行了验证)。
设计与实现损失函数¶
对于这样的模型,如何度量输出值 \(\hat{y} = f(x)\) 与真实值 \(y\) 之间的损失 \(l\) 呢? 请顺着下面的思路进行思考:
最容易想到的做法是直接计算误差(Error),即对每个 \((x_i, y_i)\) 和 \(\hat{y_i}\) 有 \(l_i = l(\hat{y_i},y_i) = \hat{y_i} - y_i\).
这样的想法很自然,问题在于对于回归问题,上述形式得到的损失 \(l_i\) 是有正有负的, 在我们计算平均损失 \(l = \frac{1}{n} \sum_{i}^{n} (\hat{y_i} - y_i)\) 时会将一些正负值进行抵消, 比如对于 \(y_1 = 50, \hat{y_1} = 100\) 和 \(y2 = 50, \hat{y_2} = 0\), 得到的平均损失为 \(l = \frac{1}{2} \big( (100 - 50) + (0 - 50) \big) = 0\), 这并不是我们想要的效果。
我们希望单个样本上的误差应该是可累积的,因此它需要是正值,同时方便后续计算。
可以尝试的改进是使用平均绝对误差(Mean Absolute Error, MAE): \(l = \frac{1}{n} \sum_{i}^{n} |\hat{y_i} - y_i|\)
但注意到,我们优化模型使用的是梯度下降法,这要求目标函数(即损失函数)尽可能地连续可导,且易于求导和计算。 因此我们在回归问题中更常见的损失函数是平均平方误差(Mean Squared Error, MSE):
\[l = \frac{1}{n} \sum_{i}^{n} (\hat{y_i} - y_i)^2\]注解
一些机器学习课程中可能会为了方便求导时抵消掉平方带来的系数 2,在前面乘上 \(\frac{1}{2}\), 本教程中没有这样做(因为 MegEngine 支持自动求导,可以和手动求导过程的代码进行对比);
另外我们可以从概率统计视角解释为何选用 MSE 作为损失函数: 假定误差满足平均值 \(\mu = 0\) 的正态分布,那么 MSE 就是对参数的极大似然估计。 详细的解释可以看 CS229 的 讲义 。
如果你不了解上面这几点细节,不用担心,这不会影响到我们完成本教程的任务。
我们假定现在通过模型得到了 4 个样本上的预测结果 pred, 现在来计算它与真实值 real 之间的 MSE 损失:
>>> pred = np.array([3., 3., 3., 3.])
>>> real = np.array([2., 8., 6., 1.])
>>> np_loss = np.mean((pred - real) ** 2)
>>> np_loss
9.75
在 MegEngine 中对常见的损失函数也进行了封装,这里我们可以使用 square_loss:
>>> mge_loss = F.nn.square_loss(Tensor(pred), Tensor(real))
>>> mge_loss
Tensor(9.75, device=xpux:0)
注意:由于损失函数(Loss function)是深度学习中提出的概念,因此相关接口应当通过 functional.nn 调用。
参见
如果你不理解上面的操作,请参考 元素级别运算(Element-wise) 或浏览对应的 API 文档;
更多的常见损失函数,可以在 损失函数 找到。
完整代码实现¶
我们同时给出 NumPy 实现和 MegEngine 实现作为对比:
在 NumPy 实现中需要手动推导 \(\frac{\partial l}{\partial w}\) 与 \(\frac{\partial l}{\partial b}\), 而在 MegEngine 中只需要调用
gm.backward(loss)即可;输入数据 \(x\) 是形状为 \((100,)\) 的向量(1 维数组), 与标量 \(w\) 和 \(b\) 进行运算时,后者会广播到相同的形状,再进行计算。 这样利用了向量化的特性,计算效率更高,相关细节可以参考 对 Tensor 进行广播 。
NumPy
import numpy as np
x, y = get_point_examples()
w = 0.0
b = 0.0
def f(x):
return w * x + b
nums_epoch = 5
for epoch in range(nums_epoch):
# optimzer.clear_grad()
w_grad = 0
b_grad = 0
# forward and calculate loss
pred = f(x)
loss = ((pred - y) ** 2).mean()
# backward(loss)
w_grad += (2 * (pred - y) * x).mean()
b_grad += (2 * (pred - y)).mean()
# optimizer.step()
lr = 0.01
w = w - lr * w_grad
b = b - lr * b_grad
print(f"Epoch = {epoch}, \
w = {w:.3f}, \
b = {b:.3f}, \
loss = {loss:.3f}")
MegEngine
import megengine.functional as F
from megengine import Tensor, Parameter
from megengine.autodiff import GradManager
import megengine.optimizer as optim
x, y = get_point_examples()
w = Parameter(0.0)
b = Parameter(0.0)
def f(x):
return w * x + b
gm = GradManager().attach([w, b])
optimizer = optim.SGD([w, b], lr=0.01)
nums_epoch = 5
for epoch in range(nums_epoch):
x = Tensor(x)
y = Tensor(y)
with gm:
pred = f(x)
loss = F.nn.square_loss(pred, y)
gm.backward(loss)
optimizer.step().clear_grad()
print(f"Epoch = {epoch}, \
w = {w.item():.3f}, \
b = {b.item():.3f}, \
loss = {loss.item():.3f}")
二者应该会得到一样的输出。
由于我们使用的是批梯度下降策略,每次迭代(Iteration)都是基于所有数据计算得到的平均损失和梯度进行的。 为了进行多次迭代,我们要重复多趟(Epochs)训练(把数据完整过一遍,称为完成一个 Epoch 的训练)。 而在批梯度下降策略下,每趟训练参数只会更新一个 Iter, 后面我们会遇到一个 Epoch 迭代多次的情况, 这些术语在深度学习领域的交流中非常常见,会在后续的教程中被反复提到。
可以发现,经过 5 趟训练(经给定任务 T过 5 次迭代),我们的损失在不断地下降,参数 \(w\) 和 \(b\) 也在不断变化。
Epoch = 0, w = 3.486, b = -0.005, loss = 871.968
Epoch = 1, w = 4.508, b = 0.019, loss = 86.077
Epoch = 2, w = 4.808, b = 0.053, loss = 18.446
Epoch = 3, w = 4.897, b = 0.088, loss = 12.515
Epoch = 4, w = 4.923, b = 0.123, loss = 11.888
通过一些可视化手段,可以直观地看到我们的直线拟合程度还是很不错的。
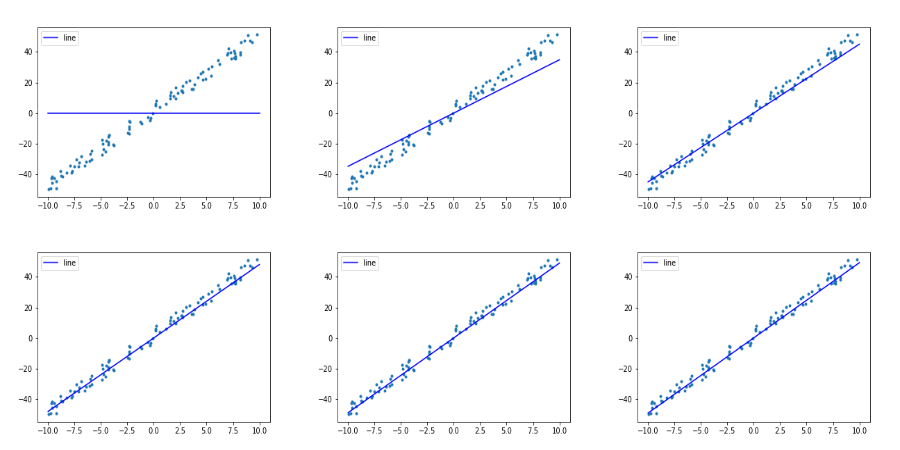
这是我们 MegEngine 之旅的一小步,我们已经成功地用 MegEngine 完成了直线拟合的任务!
参见
总结:一元线性回归¶
我们尝试用专业的术语来定义:回归分析只涉及到两个变量的,称一元回归分析。 如果只有一个自变量 \(X\), 而且因变量 \(Y\) 和自变量 \(X\) 之间的数量变化关系呈近似线性关系, 就可以建立一元线性回归方程,由自变量 \(X\) 的值来预测因变量 \(Y\) 的值,这就是一元线性回归预测。 一元线性回归模型 \(y_{i}=\alpha+\beta x_{i}+\varepsilon_{i}\) 是最简单的机器学习模型,非常适合入门。 其中随机扰动项 \(\varepsilon_{i}\) 是无法直接观测的随机变量,也即我们上面生成数据时引入的噪声。 我们根据观察已有的数据点去学习出 \(w\) 和 \(b\), 得到了样本回归方程 \(\hat{y}_{i}= wx_{i}+b\) 作为一元线性回归预测模型。
一元线性回归方程的参数估计通常会用到最小平方法(也叫最小二乘法,Least squares method)
求解正规方程的形式去求得解析解(Closed-form expression),本教程不会介绍这种做法;
我们这里选择的方法是使用梯度下降法去迭代优化调参,
一是为了展示 MegEngine 中的基本功能如 GradManager 和 Optimizer 的使用,
二是为了以后能够更自然地对神经网络这样的非线性模型进行参数优化,届时最小二乘法将不再适用。
这时候可以提及 Tom Mitchell 在 《 Machine Learning 2》 一书中对 “机器学习” 的定义:
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
如果一个计算机程序能够根据经验 E 提升在某类任务 T 上的性能 P, 则我们说程序从经验 E 中进行了学习。
在本教程中,我们的任务 T 是尝试拟合一条直线,经验 E 来自于我们已有的数据点, 根据数据点的分布,我们自然而然地想到了选择一元线性模型来预测输出, 我们评估模型好坏(性能 P)时用到了 MSE 损失作为目标函数,并用梯度下降算法来优化损失。 在下一个教程中,我们将接触到多元线性回归模型,并对机器学习的概念有更加深刻的认识。 在此之前,你可能需要花费一些时间去消化吸收已经出现的知识,多多练习。
任务,模型与优化算法
机器学习领域有着非常多种类的模型,优化算法也并非只有梯度下降这一种。 我们在后面的教程中会接触到多元线性回归模型、以及线性分类模型, 从线性模型过渡到深度学习中的全连接神经网络模型; 不同的模型适用于不同的机器学习任务,因此模型选择很重要。 深度学习中使用的模型被称为神经网络,神经网络的魅力之一在于: 它能够被应用于许多任务,并且有时候能取得比传统机器学习模型好很多的效果。 但它模型结构并不复杂,优化模型的流程和本教程大同小异。 回忆一下,任何神经网络模型都能够表达成计算图,而我们已经初窥其奥妙。
尝试调整超参数
我们提到了一些概念如超参数(Hyperparameter),超参数是需要人为进行设定,通常无法由模型自己学得的参数。 你或许已经发现了,我们在每次迭代参数 \(w\) 和 \(b\) 时,使用的是同样的学习率。 经过 5 次迭代后,参数 \(w\) 已经距离理想情况很接近了,而参数 \(b\) 还需继续更新。 尝试改变 lr 的值,或者增加训练的 Epoch 数,看损失值能否进一步地降低。
损失越低,一定意味着越好吗?
既然我们选择了将损失作为优化目标,理想情况下我们的模型应该拟合现有数据中尽可能多的个点来降低损失。 但局限之处在于,我们得到的这些点始终是训练数据,对于一个机器学习任务, 我们可能会在训练模型时使用数据集 A, 而在实际使用模型时用到了来自现实世界的数据集 B. 在这种时候,将训练模型时的损失优化到极致反而可能会导致过拟合(Overfitting)。
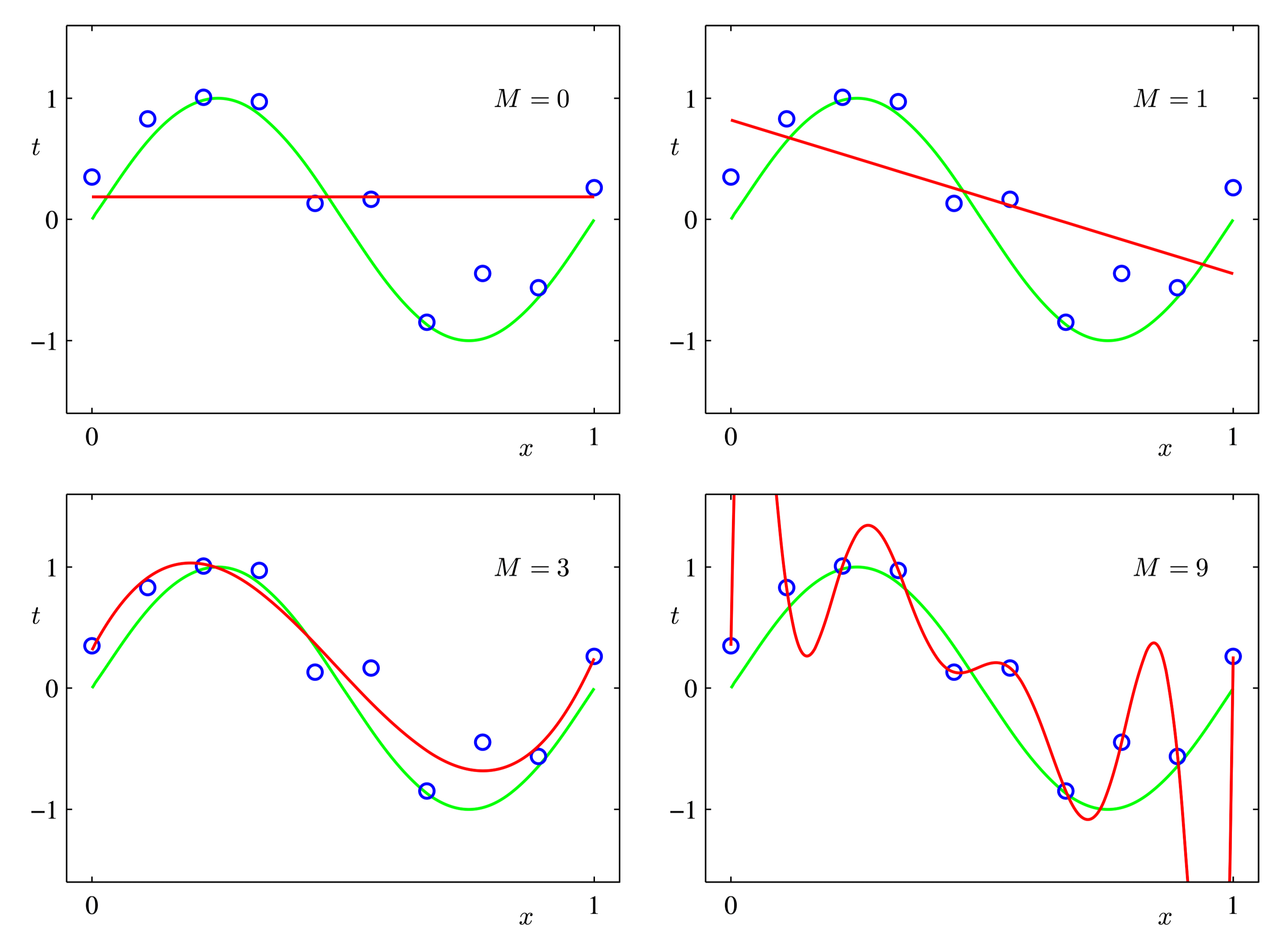
Christopher M Bishop Pattern Recognition and Machine Learning 3 - Figure 1.4¶
上图中的数据点分布其实来自于三角函数加上一些噪声,我们选择多项式回归模型并进行优化, 希望多项式曲线能够尽可能拟合数据点。可以发现当迭代次数过多时,会出现最后一张图的情况。 这个时候虽然在现有数据点上的拟合程度达到了百分百(损失为 0),但对于新输入的数据, 其预测性能可能还不如早期的训练情况。因此,不能光靠训练过程中的损失函数来作为模型性能的评估指标。
我们在后续的教程中,会给出更加科学的解决方案。
拓展材料¶
关于向量化优于 for 循环的简单验证
在 NumPy 内部,向量化运算的速度是优于 for 循环的,我们很容易验证这一点:
import time
n = 1000000
a = np.random.rand(n)
b = np.random.rand(n)
c1 = np.zeros(n)
time_start = time.time()
for i in range(n):
c1[i] = a[i] * b[i]
time_end = time.time()
print('For loop version:', str(1000 * (time_end - time_start)), 'ms')
time_start = time.time()
c2 = a * b
time_end = time.time()
print('Vectorized version:', str(1000 * (time_end - time_start)), 'ms')
print(c1 == c2)
For loop version: 460.2222442626953 ms
Vectorized version: 3.6432743072509766 ms
[ True True True ... True True True]
背后是利用 SIMD 进行数据并行,互联网上有非常多博客详细地进行了解释,推荐阅读:
同样地,向量化的代码在 MegEngine 中也会比 for 循环写法更快,尤其是利用 GPU 并行计算时。
Scikit-learn 文档:欠拟合和过拟合
Scikit-learn 是非常有名的 Python 机器学习库,里面实现了许多经典机器学习算法。 在 Scikit-learn 的模型选择文档中,给出了解释模型欠拟合和过拟合的代码:
https://scikit-learn.org/stable/auto_examples/model_selection/plot_underfitting_overfitting.html
感兴趣的读者可以借此去了解一下 Scikit-learn, 我们在下一个教程中会用到它提供的数据集接口。
参考文献¶
- 1
Charles R. Harris, K. Jarrod Millman, Stéfan J. van der Walt, Ralf Gommers, Pauli Virtanen, David Cournapeau, Eric Wieser, Julian Taylor, Sebastian Berg, Nathaniel J. Smith, Robert Kern, Matti Picus, Stephan Hoyer, Marten H. van Kerkwijk, Matthew Brett, Allan Haldane, Jaime Fernández del Río, Mark Wiebe, Pearu Peterson, Pierre Gérard-Marchant, Kevin Sheppard, Tyler Reddy, Warren Weckesser, Hameer Abbasi, Christoph Gohlke, and Travis E. Oliphant. Array programming with NumPy. Nature, 585(7825):357–362, September 2020. URL: https://doi.org/10.1038/s41586-020-2649-2, doi:10.1038/s41586-020-2649-2.
- 2
Thomas M. Mitchell. Machine Learning. McGraw-Hill, Inc., USA, 1 edition, 1997. ISBN 0070428077.
- 3
Christopher M. Bishop. Pattern Recognition and Machine Learning (Information Science and Statistics). Springer-Verlag, Berlin, Heidelberg, 2006. ISBN 0387310738.